# Robot Path Planning
In general, research on various robots can be divided into three categories of design and manufacture, navigation and guidance, and their application.
Whatever the mission of the robot, it doesn't have any impact on the role of navigation and the guidance of the robot. Given the wide extent of research in the field of navigating and guidance the robot, it breaks into four general areas of
- Positioning
- Path planning (routing)
- Motion planning (control)
- Mapping
Internet Search
Even before the development of robots, two well-known issues such as the "Traveling Salesman Problem" and "Piano Mover's Problem" have been around for many years and have been solved in various ways.me case, these applications can be transferred onto the physical robot (or rebuilt) without modifications.
Generally, a robot must proceed to calculate positions for conducting navigation and guidance. These positions could be quantitative (namely, coordinates in terms of unit length) or symbolic (such as color signs, etc.).
After this step, the robot should identify a route or path based on their current position, destination position (target) and the perception from the environment (whether with or without a map). How to specify the path is called "path planning".
After identifying path, the robot must be controlled such that it moves along this path. Robot motion control, is referred as motion planning. Some of the robots, including humanoid robots map their environment so they can use the map for their next routing purpose.
According to the available information from the environment, robotic path planning can be divided into three general categories of path planning in a known environment, path planning in a semi-known environment, and path planning in an unknown environment.
# Map representations
In order to plan a path, we somehow need to represent the environment in the computer. We differentiate between two complementary approaches: discrete (Relational representation) and continuous approximations (Coordinate-based representation).
In a discrete approximation, a map is sub-divided into chunks of equal (e.g., a grid or hexagonal map) or differing sizes (e.g., rooms in a building). The latter maps are also known as topological maps.
Discrete maps lend themselves well to a graph representation. Here, every chunk of the map corresponds to a vertex (also known as “node”), which are connected by edges, if a robot can navigate from one vertex to the other. Discrete maps are the dominant representation in robotics.
# Types of Relational representation
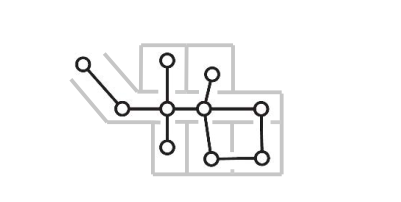
# View graph representations
In view graph representations the nodes are directly associated with the particular sen- sor input, called a view, available at a particular location.
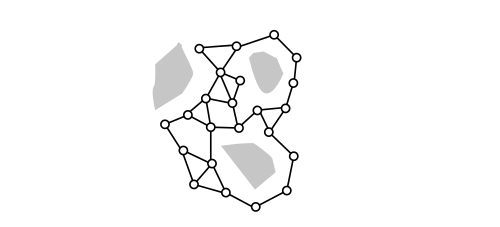
# Route Graph Representations
A general model for environmental knowledge gained by integrating route information into sur- vey knowledge by humans and animals, and also by artificial agents. We adopt it here for graph representations in which the nodes stand for distinctive places induced by the environment. The edges reflect distinctive paths connecting these places, allowing travel from one place to another.
A continuous approximation requires the definition of inner (obstacles) and outer boundaries, typically in the form of a polygon, whereas paths can be encoded as sequences of real numbers.
Currently the most common map is the occupancy grid map. In a grid map, the environment is discretized into squares of arbitrary resolution, e.g. 1cm x 1cm, on which obstacles are marked.
# Types of Coordinate Based Representations
# Occupancy Based Representations
Occupancy-based representations represent occupied and free parts of space equitably by decomposing space into cells and storing for each cell whether it is (at least par- tially) occupied or (entirely) free. Typically, the decomposition is independent of the distribution of objects in space and uniform in the sense that all cells have the same shape and size.
# Geometric Representations
Geometric representations use parameterized primitive geometric objects, i.e., points, lines, curves, planes, etc. For these objects, we will adopt the term geom here. A geometric representation basically consists of a list of geoms describing the boundaries of free space located in a single coordinate system. Most approaches used for mobile robots employ a single kind of geom.
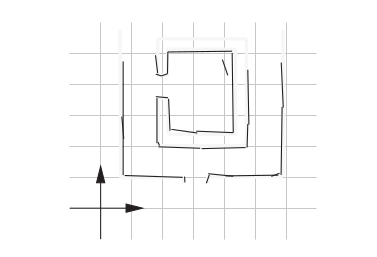
# Landmark-Based Representations
Landmark-based representations represent the world as a set of salient objects (the landmarks) extracted from the sensor data.
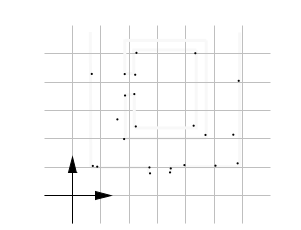
There is no silver bullet, and each application might require a different solution that could be a combination of different map types.
# Simulator Map representation
We will be using Coordinate based representation Occupancy Based Representations for our simulated environment.
For this we have to form grid , We can also perform planning in pixel basic grid but it takes a lot of computation power and complex map representation.
# Size of grid (Speed VS Accuracy)
# Path Planning Algorithms
# Dijkstra’s algorithm
Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks
# Dijkstra's algorithm to find the shortest path between a and b.
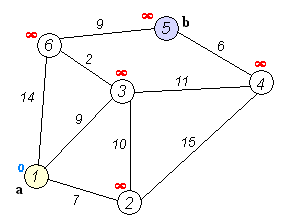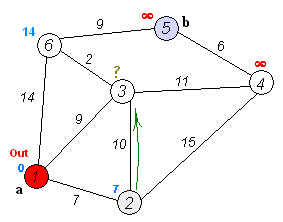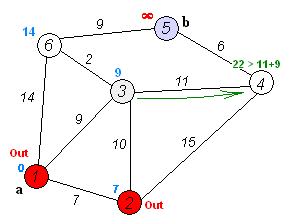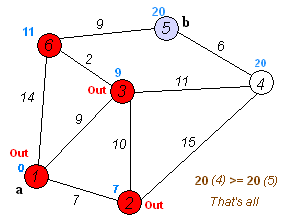
It picks the unvisited vertex with the lowest distance, calculates the distance through it to each unvisited neighbor, and updates the neighbor's distance if smaller. Mark visited (set to red) when done with neighbors.